그래프 라플라스 변환
라플라스변환 문제는 다양하게 출제되는데, 그 중에서 간단한 그래프를 제시하고 라플라스 변환 하라는 문제가 종종 출시된다.

문제를 푸는 방법은 매우 간단하다! 그림1 그래프를 먼저 단위함수로 표현한다.
y축이 변하는 지점(t=a, b)의 개수대로 항이 생성된다.(매우중요)
sol1)
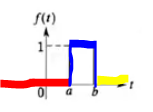
t=a인 지점에서 f(t) 값의 변화량은 +1이다.(t<a 지점에서는 계속 0 이다가, t=a지점에서 1이 된다) 그 변화량을 단위함수 앞에 곱해준다.
⇒ 1·u(t-a) ························· 식1
t=b인 지점에서 f(t)값이 1에서 0으로 -1만큼 변하므로 단위계단 함수앞에 -1을 곱해준다
⇒ -1·u(t-b) ·························식2
sol2) 각 각 위치의 단위계단함수를 다 더해준다
⇒ 1·u(t-a) -1·u(t-b) ·························식3
sol3) 단위계단함수의 라플라스 변환은 1/s 이고, 시간추이정리에 의해 식3을 변환하면

를 구할 수 있다.
하나의 예제를 더 풀어서 완벽히 이해해보자

sol1) t=0 지점에서 v(t)의 값이 0에서 1로 변화하는것을 발견하였다.
⇒ 1·u(t-0) ························· 식1
t=T 지점에서 v(t)의 값이 +1에서 -1로 -2만큼 변화하는것을 발견하였다.
⇒ -2·u(t-T) ························· 식2
t=2T 지점에서 v(t)의 값이 -1에서 +1로 +2만큼 변화하는것을 발견하였다.
⇒ +2·u(t-2T) ························· 식3
t=3T 지점에서 v(t)의 값이 +1에서 0으로 -1만큼 변화하는것을 발견하였다.
⇒ -1·u(t-3T) ························· 식4
sol2) 식1~4를 모두 더한다
⇒ 1·u(t-0)-2·u(t-T)+2·u(t-2T)-1·u(t-3T)
= u(t)-2u(t-T)+2u(t-2T)-u(t-3T)
여기서 중요한것은, 0의 지점에서도 변화량을 꼭 빼지 않고 계산해야 된다는 것이다.(식1을 빼먹지 말자)